Тетерин Г.Н.
«Откуда есть пошла» геодезия?
Геодезия настолько древняя наука, что возникает вопрос о ее начальной ступени эволюции. Приведенное название статьи, перефразирующее известное летописное выражение, характеризует проблему истоков геодезии. Во многом объяснение рассматриваемого вопроса вытекает из терминологии древнего времени касательно соответствующей системы знаний. Впервые термины геометрия и геодезия в греческой этимологии, соответственно землемерие и землеразделение, встречаются у Аристотеля в его «Метафизике». В этой работе он, возможно, не впервые утверждает различие этих понятий и их соответственно применение к «умопостигаемым» (т.е. абстрактным) , и «чувственным» объектам. Тем самым геометрия, возможно, с этого времени определяется как теоретическая, абстрактная система знаний, а геодезия — прикладная геометрия. Кстати, у Аристотеля на той же странице отмечено, что геодезия используется для определения площадей, угодий.
Греки не отрицали, что геометрия берет начало в египетском землемерии. Это и понятно, начиная с Фалеса они посещали Египет и проходили «школы» у жрецов и писцов и писцов этой страны. Там было чему поучиться. В Британском музее хранится папирус Ринда, содержащий 84 землемерных задачи, записанных (1800-й г. до н.э.) писцом Ахмесом. При этом он отмечает, что они переписаны с учебного пособия двухсотлетней давности. Таким образом эти сведения еще в 3-ем тысячелетии до н.э. использовались в писцовых школах.
Хотя понятия геометрия и геодезия идентичны, но геодезия все-таки определяет землеразделительную систему знаний, применявшуюся в задачах разделения земель, отвода земель, т.е. всю совокупность задач по землеустройству, организации земледелия, земельного кадастра. К геометрии, как системе землемерных знаний, относились задачи не только связанные с земледелием, но и специализированные, которые можно было бы назвать инженерно-техническими: прокладка каналов (Суэцкий — 6 в. до н.э.), пробивка туннелей (о. Самос — 6 в. до н.э.), строительство водоводов, дорог и т.д.
В эволюции геодезического знания, особенно в его древней начальной стадии, поражает некий мистический аспект, какая-то заданность, «божественность», по крайней мере, в представлениях древнего человека. Еще более приводит к какой-то предопределенности то, что эти знания зарождались под сводами храмов усилиями жрецов и потому наделялись эпитетами «святости», «священности». Необъяснимость возникновения такого рода (геометрического) знания зарождалась и развивалась во времена глубокой древности, а также античности древними эллинами.
Вся геометрия древнего времени носила сакральный смысл. В то же время эта геометрия имела несомненную геодезическую принадлежность и геодезический смысл, вполне объяснимый в плане использовавшихся терминов — геометрия и геодезия (землеразделение). В древнее время основным производством являлось земледелие. Оно составляло основу процветания государства, его жизненной устойчивости и богатства. В свою очередь, основу организации производства, его успешности составляло землемерие, на основе которого формировался земельный кадастр. Таким образом, все творческие силы и труд древних людей были направлены на решение задач, связанных с землеразделением, его организацией. В этой сфере, если не главной его частью, то по крайней мере важнейшей, было разделение земли на участки (геодезия — землеразделение), т.е. система межевания, ее геометрия. Из нее вытекали в частности такие задачи как восстановление границ земельных наделов после разливов рек (Нила, Тигра, Евфрата и др.), проведение новых границ при делении наделов в результате наследственных разделов или государственных «дарений» и т.д. Во всех случаях важным была оценка площади земельных угодий. Все перечисленное составляло в совокупности сложную геометрическую проблему древнего времени. Таким образом поддержание всей системы земледелия в должном порядке являлось главной задачей того времени. Поэтому сложности землемерия и соответствующие знания составляли важнейшую отрасль технических и практических знаний. Значимость всего этого подтверждалось текстами и рисунками на стенах храмов, усыпальниц и пирамид. Геометрия одухотворялась мифологией и соотносилась с божествами, наполнялась сакральной психологией. Терминология древнего исходного геодезического знания в какой-то мере показывает «откуда есть пошла» геодезия.
В построенной среде обитания (землеустройство, строительство), ее безусловным и безоговорочном требованием является геометрический язык. Основой этого языка служат точки, линии и поверхности. Их главной комбинацией служат три фигуры: квадрат, треугольник и круг. В древнее время китайцы говорили: «Небо представляется кругом, земля — квадратом». Геометрическим фигурам приписывались свойства и качества, являвшиеся атрибутом человека и общества. Прокл Диадох (485-410), считавший круг совершенной фигурой, говорил: «Если разделить Вселенную на небеса и бренный мир, то круговые формы надлежит приписывать небесам, а прямые — бренному миру…». Пифагорийцы утверждали, что «квадрат несет образ божественной природы, и он несет в себе высокое достоинство, так как прямизна углов передает целостность, а качество сторон способно устоять перед силой». Познание и освоение пространственно-временных свойств окружающей среды определяло необходимость формирования и развития знаний о геометрии окружающей среды. Форма, размер, пространственное положение (ФРПП), объектов и явлений окружающей среды жизненно необходимой человеку, чтобы организовать свою ойкумену.
Во всех древних цивилизациях, начиная с 4-го тысячелетия до н.э., а возможно и ранее, деление земельных угодий на отдельные участки, производилось системой межевых линий на квадраты. Эта фигура являлась наиболее приемлемой в плане организации земельных угодий и по причине, что квадрат как геометрическая фигура наиболее проста и по форме, и по доступности для понимания. Эта система межевания, деления общих площадей земельных угодий подтверждается историческими данными, в том числе известным указом египетского фараона Сизостриса. Образцом такого деления земельных угодий являлся римский кадастр; его геометрическая схема деления земли на центурии (квадратные формы) представлена на рис. 1. В таком центурийном поле определились две центральные перпендикулярные друг другу оси (кардо и декуманус максимум), а все центурии полученные на местности имели двойную (координатную) нумерацию [1, 3].
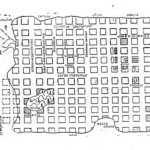 Рис. 1. Деление земли на центурии.
Рис. 1. Деление земли на центурии.
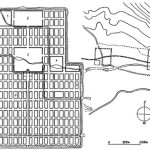
Помимо земледелия геометрические знания стали широко применяться при строительстве городов. Система прямоугольной (поквартальной) планировки городов стала в какой-то мере нормой в строительстве городов древнего мира со времен Греции, ее архитектора Гипподама (V в. до н.э.). в то же время такая планировка застройки городов встречалась много ранее в Индии и в Китае. В частности, характерна планировка г. Лоян (рис. 2) в древнем Китае. В китайском трактате «Чжоу ли», содержащем сведения о городах XII-IX вв. до н.э., сообщается, «что столичный Лой (Лоян) был квадратным в плане, имел девять широтных и девять меридиональных улиц» [1, 2].
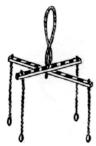
Квадрат был также главной планировочной основой в храмовом строительстве. Структурной основой задачи построения квадрата на земле является прямой угол. Вся технология земельного кадастра заключалась в использовании средств, инструментов, способов построения прямого угла. В истоках землемерной технологии деления участков на квадраты, был сам человек, его «прямоугольная» фигура. Этот метод деления описан в книге [5]. Позднее стали использовать так называемые землемерные кресты: египетский (рис. 3) и римский (грома, рис. 4). последняя использовалась в землеустройстве, строительстве городов, храмов и дорог. Кстати, специалистов, работавших с этим прибором называли громатиком.
Важно отметить, что в 3-ем тысячелетии до н.э. В Египетском фундаментальном храмовом и сакральном строительстве точность построения квадратного основания Гизехских пирамид была много выше, чем могло быть получено с помощью землемерных крестов, упомянутых выше. Пирамиды Хеопса, Хефрена, Микерина стоят до сих пор, потому, что жесткость их постройки обеспечена в том числе геометрически правильным и точным квадратным основанием. Гиптяне добились высокой точности построения прямоугольных фигур на земле, потому что ими, как и вавилонянами был открыт прямоугольный треугольник с соотношннием сторон 3: 4: 5, удовлетворявшим условию: сумма квадратов катетов равна квадрату гипотенузы (a2+b2=c2). Доказательство этого факта было дано Пифагором спустя 2000 лет. Загадка — как жрецы древнего Египта смогли открыть этот «закон» геометрии? Используя правило такого треугольника (греки называли его египетским) был создан веревочный «шаблон» (мерная веревка с узлами на помеченных отрезках длины соответственно 3, 4, 5). С его помощью было просто строить прямой угол и при делении земельных угодий на отрезки, и при разбивке основания пирамид, и при всех других случаях, где нужно было построить прямой угол.
Главной задачей в строительстве является построение прямого угла, а это определяет прочность сооружения. Наилучшая форма основания сооружения — квадрат, а проекция центра тяжести постройки на середину основания (точку пересечения диагоналей квадрата) создает идеально устойчивую конструкцию. Именно так построены египетские пирамиды, буддийские ступы, башни, столпообразные и крестово-купольные храмы. В этих примерах проявляется взаимосвязь закономерностей земной гравитации, симметрии и пропорции.
Гимей отмечал, что истинными элементами материального мира являются не земля, воздух, огонь и вода, но два вида прямоугольных треугольников: половина квадрата и половина равностороннего треугольника. Этот треугольник являлся основой разнообразного инженерного применения в том числе в архитектуре. С помощью такого треугольника с его использованием решалось большинство задач практической геометрии (геодезии древнего времени), перечисленных в перечне 17 задач Герона Александрийского.
Структурной основой упомянутых двух фигур (квадрат, прямоугольный треугольник) был прямой угол. Следует заметить, что прямоугольность является универсальным и повсеместным свойством окружающей среды. Ключом к решению большинства землемерных (землеустроительных), строительных и архитектурных задач был прямой угол. Его реализация в выполнении геометрических построений на земле (в земледелии, инженерном и архитектурном строительстве) была основополагающим фактом. Требовалась материализация, овеществление этой фигуры в каком-либо предметном исполнении. Для полного решения задачи уже в глубокой древности, как было отмечено выше, «чудесным» образом был открыт священный треугольник со сторонами 3, 4, 5 единиц длины.
Несомненно, простота вещественного построения прямоугольного треугольника и реализация соответствующих функциональных (геодезических), а также геометрических задач в строительстве вообще и в архитектуре в частности, составляла важнейшую проблему того времени. Одним из важнейших средств построения геометрических фигур является прямоугольный треугольник. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей (тройка чисел, отвечавших теореме Пифагора). Пирамиды фараона Снофру (XXVII в. до н.э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей. Все это характеризовало божественное происхождение прямоугольного треугольника, некий священный смысл. Таким образом, вещественная или материализованная фигура прямого угла, да и сам прямой угол, как геометрическая фигура (в теории) служили таинственным ключом к постижению окружающего мира и построению своей ойкумены, своей среды обитания.
Все параметры египетского треугольника: числа 3, 4, 5; угол 53º08´ являлись стандартом Древнего Египта при проектировании различных сооружений, в том числе пирамид, а также при размежевании полей.
Числа пифагоровой тройки, в том числе 3, 4, 5 и т.д. входят в «золотой ряд» (золотое сечение): 1, 1, 2, 3, 5, 8, 13, 21, … В этом ряду каждый последующий член равен сумме двух предыдущих: 1+1=2, 1+2=3, 2+3=5, 3+5=8 и т.д. Следовательно, египетский треугольник имеет отношение к золотому сечению. Золотой ряд впервые опубликовал в 1202 г. Леонардо Пизанский (Фибоначчи, 1180-1240). В XV в. Леонардо да Винчи (а также Пачиоли) впервые ввели выражение золотое сечение («божественная пропорция»). Следует заметить, что золотое сечение было известно Пифагору и его ученикам, хотя называлось оно по другому, как «деление в среднем и крайнем отношении». Весь видимый мир, в пределах земной гравитации следует законам симметрии, энтропии; его структура выражается рядом Фибоначчи и золотой (божественной) пропорцией. А египетский треугольник с его «золотым сечением» был известен еще в Древнем Египте, когда строились Великие пирамиды.
Очевидно, все в мире подчиняется «золотому правилу». И всякое искусственное его нарушение приводит к искажению законов природы и космоса, вносят дисгармонию в окружающее пространство. Задача о построении прямоугольника фактически может решаться способом деления отрезка в крайнем и среднем отношении. Название этому треугольнику (египетский) дали греки, которые в VII-V вв. до н.э. посещали Египет. Жрецы Египта треугольник со сторонами a, b, c, отвечавшими требованию a2+b2=c2, именовали «священным». Он символизировал великую триаду богов: Исида, Осирис и их сын Гор (два катета и гипотенуза, олицетворяемая Гором-Соколом.
«Золотое число» (функция золотого сечения) обозначается буквой φ («фи», где φ=1,618 — в честь знаменитого греческого скульптора Фидия). Числами Фибоначчи (его ряда) по Ньютону и Кеплеру определяются радиусы и периоды обращения планет вокруг Солнца. При проектных, разметочных и строительных работах в конструкции пирамид и других сложных сооружений закладывались пропорции треугольника со сторонами 3, 4, 5 и углами 36º34´ и 53º08´.
В работе В.П. Бабанина [http://www.shaping.ru/mku/babanin02.asp] приведены знаменательные и характерные выражения, касающиеся рассматриваемого треугольника: «… знаменитый египетский треугольник с соотношением сторон 3: 4: 5 «взят» из молекулы воды. Сама же геометрия молекулы воды образована двумя египетскими треугольниками, имеющими общий катет, равный 3. Истинным создателем молекулы воды, а значит и египетского треугольника, является сама природа. Именно поэтому в них заложена та гармония, которая присуща всему космосу, и которая выражается, в частности, свойствами золотого сечения. Только этим можно объяснить, почему древние египтяне обожествляли числа 3, 4, 5, а сам треугольник считали священным и буквально «нянчились» с ним, как с младенцем, стараясь заложить в любую конструкцию, в пирамиды, даже в разметку полей его божественные свойства, его гармонию» [http://www.shaping.ru/mku/babanin04.asp].
В заключении отметим, что зарождение геодезии соотносится с возникновением земледельческих, городских цивилизаций (4-3 тыс. до н.э.). Именно в это время возникает потребность деления земельных угодий на участки. Этот факт хорошо иллюстрируется легендой о мифическом фараоне Сизострисе, повелевшем разделить всю землю Египта на квадратные участки, раздать их земледельцам и взимать с них соответствующие налоги. Это служит исторической датой зарождения земельного кадастра, зарождения геодезии как землеразделительной системы практических, а затем и теоретических знаний. В третьем же тысячелетии до н.э. указами месопотамского повелителя Саргона были введены общие (государственные) единые меры, необходимые для оценки площадей. При делении площадей стала необходимой геометрия, в соответствии с которой определялись формы и размеры геометрических фигур. Для решения важнейшей государственной на то время задачи наилучшей по размеру и форме (по подсчету площадей) стал квадрат, а затем и треугольник, о чем выше сказано.
Таким образом, геометрия (землемерие) и стала исходным временем появления геодезического знания. Вся сакральная геометрия, по существу, это и есть геодезия, предметные свойства которой (форма, размер) стали основой ее зарождения.
Вместе с тем, вся совокупность математических и геометрических знаний появилась в это время как бы «неожиданно», без логики и последовательности развития. Появились формулы подсчета площадей различных фигур, правила подсчета различных пропорций, в том числе «божественной», постоянных: φ=1,618 (золотое правило), π=3,14 (как соотношение между длиной окружности и диаметром). Но еще более поразительно, что вавилоняне и египтяне открыли прямоугольный треугольник с соотношением сторон a²+b²=c² (3, 4, 5 единиц длины). Доказательство такого треугольника было дано двумя тысячелетиями позже Пифагором. Бездоказательная совокупность всего геометрического знания Древнего Египта и Вавилона вполне соотносится с его божественностью и сакральностью. Эти знания охранялись покровительством богов древнего мира, им возносились молитвы, им приносились жертвы на межевых знаках. Доказательная геометрия появилась в первом тысячелетии до н.э. Благодаря трудам Фалеса (624 -548), Пифагора (570-490), Платона (427-347), Евклида (365-300) и др. Таким образом, рассматриваемая историческая эпоха (4-3 тыс. до н.э.) дают ответ на вопрос, вынесенный в заголовок статьи.
Список литературы
- Тетерин Г . Н . История геодезии в градостроительстве и возведении сложных сооружений. – Новосибирск: Сибпринт, 2003. – 116 с.
- Тетерин Н.Г. История межевания, землеустройства и земельного кадастра. Новосибирск: СГГА, 2007. – 98 с.
- Тетерин Г.Н., Синянская М.Л. Биографический и хронологический справочник (Геодезия до ХХ в.). — Новосибирск: Сибпринт, 2009. — 516 с.
- Тетерин Г. Н. История геодезии (до XX в.). – Новосибирск: Альянс-Регион, 2008. – 300 с.
- Бабанин В.П. Тайна великих пирамид. — Санкт-Петербург: Лань, 1999.