УДК 528 (091)
528 (092)
ЛОГИСТИЧЕСКИЙ ЗАКОН РАЗВИТИЯ ГЕОДЕЗИИ КАК ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ ПРЕДОПРЕДЕЛЕННОСТЬ
Синянская Мария Леонидовна
Сибирская Государственная Геодезическая Академия (аспирант); 630077, г. Новосибирск, ул.Станиславского 29-291; +7(913)-010-35-56; mariyateterina8888@mail.ru
В статье рассматривается теория развития геодезии в рамках теории предопределенности. Излагаются законы развития геодезии в последовательности смены парадигм. Предлагается для рассмотрения математическая модель параметров развития по историческим эпохам. Также приведены приблизительные прогнозы ближайшего развития геодезии и показан механизм определения основных переломных моментов в процессе становления геодезии.
Ключевые слова: теория предопределенности, логистический закон, коэффициент сжатия.
LOGISTICS DEVELOPMENT LAW OF SURVEYING AS A SPATIO-TEMPORAL PREDESTINATION
Sinânskaâ Maria Leonidovna
Siberian State Geodesic Academy (PhD student); 630077, Novosibirsk, Russia, Stanislavski Street 29-291; +7 (913) -010 -35 -56; mariyateterina8888@mail.ru
Describes a theory of the development of Geodesy in the theory of predestination. Set out the laws of development of Geodesy in the sequence paradigm shifts. A mathematical model for the consideration of the parameters of development of historical epochs. Provides approximate estimates of the nearest development of Geodesy and shows the mechanism of determining the major turning points in the development of Geodesy.
Keywords: theory of surveying, logistics development law of surveying, theory of predestination, compression ratio of historical time.
Процессы, проходящие в пространстве и времени подчиняются соответствующим законам и укладываются в рамки пространственно-временных отношений [2]. Эти законы и отношения вполне четко устанавливают своего рода предопределенность развития процесса, в какой-то мере его заданность. Ярким примером закона пространственно-временной предопределенности является логистический, рассматриваемый в теории развития геодезии (ТРГ). В этом законе, сформулированном Г.Н. Тетериным [12, 13, 14, 18, 24], установлена связь между историческим временем и системой геодезических знаний, в целом геодезии, ее соответствующими тенденциями и группами факторов.
Как известно [12, 13, 18], предметом геодезии являются форма, размер, пространственное положение (ФРПП). В совокупности эта триада названа геодезической метрикой [3]. Поэтому геодезию как научно-практическую систему знаний можно определить следующим образом: геодезия занимается измерением, моделированием и контролем геодезической метрики различных объектов и явлений окружающего пространства. Из определения следует, что основная функция геодезии представляется как измерение геодезической метрики [20, 22, 25]. Поэтому функция измерений является главной и обобщающей для всей геодезии. В характеристике этой функции ее эффективность и точность измерений служат важнейшими показателями геодезии. Именно для этой функции установлена ее связь со временем в виде:
у = f(i) = 10-2i, (1)
где у – функция, характеризующая эффективность системы (геодезии) в том числе точность измерений;
i – нумерация исторических событий (этапов, эпох) по оси исторического времени, т.е. i=1, 2, …, n.
Нумерация исторических эпох i характеризует взаимосвязь пространства и времени, поскольку i представляет собой ось исторического времени, на которой размещены геодезические эпохи, а вместе с ними и измерения в пространстве.
В соответствии с формулой (1) и четырьмя историческими эпохами (i = 1, 2, 3, 4), точность измерений в каждой исторической эпохе будет определяться следующим выражением:
у = f(i) = {10-2(i-1) – 10-2i} (2)
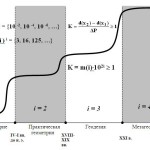
В формуле (2) в рамках рассматриваемого логистического закона величина i имеет значение: i=1 – землемерная эпоха; i=2 – геометрическая (римско-эллинистическая); i=3 – топографо-геодезическая; i=4 – геоинформационная (глобальная) [6, 8, 15, 24, 25].
Длительность четырех исторических эпох представлена на рисунке 1 [12] и в таблице 1 [7, 18, 24]. Эта длительность исчисляется для землемерной эпохи в тысячелетиях (6000-8000 лет), геометрической – тысячелетиями и столетиями (1600-1700 лет), топографо-геодезическая эпоха оценивается столетиями и десятилетиями (около 400 лет). Вместе с тем установить относительно точные границы между эпохами затруднительно, но, тем не менее, возникает потребность в такой оценке [11, 16].
Приведем метод оценки и расчетов по определению временных показателей, связанных как с отдельными историческими эпохами, так и с их последовательностью, с определением исторических границ, как в отношении прошедших эпох, так и предстоящих [4, 25].
Рис. 1. Логистический закон развития геодезии
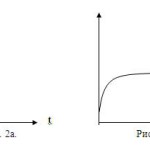
Будем полагать, что отдельная историческая эпоха характеризуется как цикл развития (рис. 1). В этом цикле выделяются революционные и эволюционные части. При этом каждый цикл можно определить в одном из двух возможных вариантов: эволюционные плюс революционные части или революционные плюс эволюционные части (рис. 2а и 2б) [25].
На рис. 2а и 2б эволюционная часть цикла представлена пологой частью кривой, а революционная – резко возрастающей вверх частью.
Таблица 1 Парадигмы
Исторические границы первого цикла (землемерной эпохи) развития установить сложно [4, 9, 10]. Последующие циклы можно сравнительно точно (относительно) определять по революционной части цикла [1]. Такие революционные части можно установить по так называемым точкам предопределенности. Такими точками являются изобретения, открытия, предопределяющие технический или технологический прогресс. По существу такие точки представляются начальными точками развития [9]. Совокупность таких точек предопределенности сравнительно полно характеризует в плане исторического времени революционную часть цикла. Тем самым она определяет границы и эволюционной части цикла (цикл предопределенности). В таблицах 2 и 3 дан список открытий, изобретений, новаций [5, 19, 23] в первом тысячелетии до н.э. (греческая революционная часть) и в середине второго тысячелетия, определивший начало топографо-геодезического цикла развития. Последующий революционный этап развития для конца третьей исторической эпохи или для начала четвертой оценивается по длительности в 50 лет.
Таблица 2 — Точки предопределенности в геометрическую эпоху
| Дата | Событие |
| V в. до н.э. | У древних греков окончательно сложилось представление о Земле как о шаре (Парменид). |
| V в. до н.э.
|
Строительство «царской дороги» Ахменидов (Персия) длиной 2,4 тыс. км (от Суз в Малую Азию). |
| IV в. до н.э. | Начало строительства акведуков. |
| IV в. до н.э. | Первая теория движения планет (Евдокс Книдский). |
| IV в. до н.э. | Первое объяснение суточного вращения Земли (Гераклид). |
| Вторая половина IV в. до н.э. | Аристотель (384-322гг. до н.э.) впервые в своей книге «Метафизика» ввел термин геодезия и определил сущность различий геометрии и геодезии. |
| 380 г. до н.э. | Первые эфемериды планет (клинописные тексты). |
| Ок. 360 г. до н.э. | Первый китайский звездный каталог. |
| Ок. 360 г. до н.э. | Геоцентрическая система мира (Аристотель). |
| Ок. 300 г. до н.э. | «Начала» Евклида. |
| IV – III вв. до н.э. | Установление размера Земли (Диккеарх Мессинский). |
| III в. до н.э.
|
Определение относительных размеров Земли, Луны, Солнца и относительных расстояний между ними (Аристарх Самосский). |
| 240 г. до н.э. | В Китае была написана «математика в девяти книгах». |
| III – II вв. до н.э. | Первое градусное определение Земли (Эратосфен, города Сиена и Александрия). |
| II в. до н.э. | Методы центуриации и скамнации в римском земельном кадастре. |
| II в. до н.э. | Гиппарх: открытие прецессии, каталоги звезд с указанием их звездных величин, географическая система координат, точные астрономические измерения. |
| II – I вв. до н.э. | Глобус Кратера из Малоса. |
| I в. до н.э. | Определение размеров Земли (Посидоний). |
| 20 г. до н.э. | Витрувий написал трактат «Десять книг об архитектуре». |
| I в. | «Золотой миллиарий» — центр Римской империи. |
| I в. | Географическая карта Римской империи (Агриппа). |
| I в. | Начало сферической тригонометрии (Менелай Александрийский). |
Таблица 3 — Точки предопределенности в топографо-геодезическую эпоху
| Дата | Событие |
| Начало XVIв. | Начало разработки и применения метода триангуляции. |
| Начало XVIв. | Начало формирования метода топографической съемки. |
| 1502-1504гг. | Первые использования масштаба при составлении плана (Леонардо да Винчи, г.Имола) |
| 1513г.
|
Разработан полиметрум Мартина Вельдземюллера – первый ранний прототип теодолита (измерение горизонтальных и вертикальных углов, П. Апиан, «Космография»). |
| 1528г.
|
Издана работа Мюнстера в которой он описал полярный метод. Углы измерялись по буссоли, расстояния шагами. |
| 1540-1570гг. | Введение масштабов на военных картах. |
| 1542г.
|
Нониус (1492-1577гг.) описал метод отсчетов мелких делений на квадранте у морской астролябии. |
| 1543г. | Гелиоцентрическая система мира Коперника. |
| 1546г.
|
Гемма Фризиус – первое описание метода триангуляции, Герард Меркатор применил его при съемках в Голландии. |
| середина XVIв.
|
Порта — камера-обскура, с помощью которой создавали перспективные рисунки местности. |
| середина XVIв. | Использование жезла Якоба в землемерии и навигации. |
| 1560-1575гг. | Якоб ванн Дервентнер — графический метод триангуляции. |
| 1563г. | Пухлер — метод трансверсалей или диагональных шкал. |
| 1570г. | Массовое использование масштабов. |
| 1571г. | В «Пантометрии» впервые использовался термин теодолит. |
| 1596г. | Издается труд Ратикуса по основам триангуляции. |
| начало ХVIIв. | Английский астроном Гаскуань (1598-1658гг.) заменил в квадрантах диоптры на зрительные трубы. |
| начало XVIIв. | Самое раннее описание экера. |
| XVIIв. | В мензульной съемке стали применять алидадную линейку с диоптрами (и масштабом). |
| 1600г. | Д.Чименти получил первую стереоскопическую пару рисунков. |
| 1603г. | Шейнер создал прибор пантограф. |
| 1609г. | Изобретение зрительной трубы. |
| 1611г. | Клавиус преобразовал нониус в отчетное устройство — верньер. |
| 1611г.
|
И.Преториусом (1537-1616гг.) создана мензула. Описана в 1618г. Д.Швентнером (1585-1636гг.). |
| 1614г. | Непер разработал метод логарифмов. |
| 1615-1616гг. | Градусные измерения Снеллиуса по методу триангуляции квадрантом с диоптрами. |
| 1633-1635гг. | Градусные измерения Норвуда (графометр, стальные цепи). |
| 1634г. | Начальный меридиан о.Ферро (Ришелье). |
| 1635-1636гг. | Разработана прямоугольная система координат (П.Ферма, Р.Декарт). |
| 1641г. | Паскаль сконструировал механическую вычислительную машину. |
| 1665г. | Ньютоном разработана теория всемирного тяготения. |
| 1666г. | Шапоти (Франция) — использование цилиндрического уровня. |
| 1670г. | Тевенот (Франция) — воздушный пузырек в уровне. |
| 1689г. | О.Ремер создал шкаловый микроскоп. |
Во второй половине ХХ века произошло полное обновление средств измерений, методов, технологий. Начиная с 50-х годов были разработаны и внедрены электронные дальномеры, одним из первых в Швеции был разработан светодальномер Геодиметр. В Советском Союзе, во второй половине 50-х годов был разработан светодальномер СВВ-1. В последующем появился высокоточный светодальномер ЭОД. В 60-70-х годах появился ряд электронных свето- и радиодальномеров, затем электронные тахеометры и множество других электронных систем измерений. В 60-х годах создавались вычислительные центры в геодезических вузах, в ЦНИИГАиКе и т.д., в которых производилась обработка и уравнивание геодезических измерений. С запуском специальных космических спутников формируются различные глобальные навигационные системы, системы дистанционного зондирования, новые системы координат [13, 21, 23]. Создаются новые технологии, автоматизированные и автоматические технологии лазерного сканирования, ГИС-технологии и т.д.
По существу все точки предопределенности этого революционного этапа развития были связаны с открытием различных электронных систем измерений, ЭВМ и компьютерами, космическими и лазерными методами и т.п.
Используя временные рамки революционных этапов последних трех эпох и длительность второй и третьей эпох, можно установить так называемый коэффициент сжатия исторического времени как в целом для циклов развития, так и для их революционных частей. Обозначим эти коэффициенты как α и β. В целом введенные коэффициенты и длительности циклов развития (ΔT) и длительности революционной части (Δt), можно сравнительно точно определить исторические даты, связанные с границами циклов развития.
Для варианта цикла «эволюция + революция» (рис. 2а) получим длительность ΔT исторических эпох вида:
ΔTi = {8300; 1670; 330} (3)
Для этих значений:
αi = ΔTi / ΔTi+1 = {8300/1670; 1670/330} = {5; 5,1}, (4)
а αср ≈ 5.
Соответственно для революционных частей циклов развития (3) получим:
Δti = {600; 170; 50} (5)
С учетом (5) получим:
βi = Δti / Δti+1 = {600/170; 170/50} = {3,5; 3,4}, (6)
а βср ≈ 3,5.
С учетом вычисленных коэффициентов α и β, а также длительности исторических эпох – (3) и революционных частей – (5) можно установить дату завершения четвертой исторической эпохи и соответствующих дат связанных с революционной частью:
Ti+1 = Ti + ΔTi-1, i /αi, (7)
где Ti – конец эпохи i;
ΔTi-1, i – продолжительность эпохи.
Примем T3 = 1990 г. (конец 3-ей эпохи). Тогда: T4 = T3 + ΔT4-3 / αср. ≈ 1990 + 330/5 ≈ 1990 + 66 ≈ 2056
Соответственно:
ti+1 = Ti + Δti-1, i / βср. (8)
и t4 = T4 – Δt4/ βср ≈ 2056- 50/3,5 ≈ 2040.
Приводимые цифры являются приближенными и округленными в пределах указанной выше точности исчисления времени T4 и t4.
Повторим аналогичный расчет для варианта цикла «революция + эволюция» (рис. 2б):
ΔT’i = {9000; 2000; 450}, (9)
Δt’i = {2000; 600; 170} (10)
α’i = ΔT’i / ΔT’i+1 = {9000/2000; 2000/450} = {4,5; 4,4}, (11)
α’ср ≈ 4,5.
β’ i = Δt’i / Δt’i+1 = {2000/600; 600/170} = {3,3; 3,5} (12)
β’ср ≈ 3,4.
В соответствии с приведенными значениями ΔT’, Δt’, α’ и β’, используя формулы (7) и (8) получим:
T’i+1 = T’i + ΔT’i-1,i/ α’ i, (13)
T’4 = T’3 + ΔT’4-3/ α’ i ≈ 1950 + 450/4,5 ≈ 2050.
t’i+1 = T’i-1 + Δt’i / β’ i, (14)
t’4 = T’3 + Δt’4-3/ β’ i ≈ 1950 + 170/3,4 ≈ 2000.
С учетом приведенных числовых значений ΔT, ΔT’, Δt и Δt’ можно найти соотношение между революционной и эволюционной частями циклов развития, тогда получим следующее:
γi = ΔTi / Δti = {8300/600; 1670/170; 330/50} = {14; 10; 7}, (15)
γ’i = ΔT’i/Δt’i = {8000/2000; 2000/600; 450/170} = {4; 3; 3}. (16)
С помощью γ и γ’ можно скорректировать временные границы циклов развития всех исторических эпох.
Представленная методика расчетов временных параметров относительно длительности эпох, соответствующих дат и их границ дает возможность оценить неравномерность развития геодезии в рамках всего исторического времени [24, 25]. Характеристиками и критериями этой неравномерности являются так называемые коэффициенты сжатия исторического времени α и β равные в среднем соответственно 5 (4,5) и 3,.5 (3,4). Эти два коэффициента являются одновременно коэффициентами предопределенности развития. Данная методика расчетов исторических процессов вполне применима к древним системам научных знаний [17, 25].
Литература
- Кун Т. Структура научных революций. – М.: Прогресс, 1977. – 300 с.
- Рейхенбах Г. Философия пространства и времени. – М.: Прогресс, 1985. – 344 с.
- Синянская М.Л. Фактор прямого угла в «Принципах влияния» в геодезии // Интерэкспо ГЕО-Сибирь-2012. VIII Междун. науч. конгр. : Междун. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия» : сб. материалов в 3 т. (Новосибирск, 10-20 апреля 2012 г.). – Новосибирск: СГГА, 2012. Т. 1. – С. 106-110.
- Синянская, М.Л. Факторы предопределенности развития геодезии // Интерэкспо ГЕО-Сибирь-2012: VIII Междунар. науч. конгр., 10–20 апреля 2012 г., Новосибирск: сб. молодых учёных СГГА. – Новосибирск : СГГА, 2012. –С.54–59.
- Синянская, М.Л. Банк данных второго поколения по истории геодезии и картографии // Геодезия и картография. – 2012. – № 6. – C. 56–61.
- Синянская М.Л. Сакральная геометрия и геодезия // Интерэкспо ГЕО-Сибирь-2013. IХ Междун. науч. конгр. : Междун. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия» : сб. материалов в 3 т. (Новосибирск, 15-26 апреля 2013 г.). – Новосибирск: СГГА, 2013. Т. 1. – С. 58-62.
- Синянская М.Л. Прямоугольность как геометрический фактор развития геодезии // Вестник СГГА. – 2013. – Вып. 1 (21). – С. 11-15.
- Синянская, М.Л. Сакральная геометрия, египетский треугольник и геодезия // Геодезия и картография. – 2013. – № 6. – C. 57–60.
- Синянская М.Л., Тетерин Г.Н. Теория развития геодезии и факторы предопределенности // Вестник СГГА. – 2014. – Вып. 1 (25). – С. 3-11.
- Синянская, М.Л. Геном геодезии и факторы предопределенности // Интерэкспо ГЕО-Сибирь-2014: X Междунар. науч. конгр., 16–18 апр. 2014 г., Новосибирск: Междунар. науч. конф. «Геодезия, геоинформатика, картография, маркшейдерия»: сб. материалов в 3 т. – Новосибирск: СГГА, 2014. – Т. 1. – C. 75–79.
- Тетерин Г.Н. Константы развития и точки прогнозирования // Вестник СГГА. – 2002. – Вып. 7. – С.
- Тетерин Г. Н. Теория развития и метасистемное понимание геодезии. Новосибирск: Сибпринт, 2006. — 162 с.
- Тетерин Г.Н. История геодезии (до XX в.). Новосибирск: ООО «Альянс-Регион» 2008 — 300 с.
- Тетерин Г.Н. История геодезии – двадцатый век (Россия, СССР) – 2010. – 403 с.
- Тетерин Г.Н., Тетерина М.Л. Древние измерительные системы и два принципа влияния (ПВГ и П4Н) // ГЕО-Сибирь-2009. V Междунар. Науч. конгр. : сб. материалов в 6 т. (Новосибирск, 20-24 апреля 2009 г.). – Новосибирск: СГГА, 2009. Т. 1, ч. 1. – С. 123-124.
- Тетерин Г.Н., Синянская М.Л. Феномен прямого угла и прямоугольности в геодезии // ГЕО-Сибирь-2010. VI Междунар. Науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2010 г.). – Новосибирск: СГГА, 2010. Т. 1, ч. 1. – С. 48-51.
- Тетерин Г.Н., Синянская М.Л. Угловые и линейные меры измерений в древнее время // ГЕО-Сибирь-2011. VII Междунар. Науч. конгр. : сб. материалов в 6 т. (Новосибирск, 19-29 апреля 2011 г.). – Новосибирск: СГГА, 2011. Т. 1, ч. 1. – С. 79-83.
- Тетерин Г.Н. Феномен и проблемы геодезии: / Тетерин Г.Н. – Новосибирск: СГГА, 2009.-95с.
- Тетерин Г.Н., Синянская М.Л. Биографический и хронологический справочник (Геодезия, до ХХ в.) – 2009. – 516 с.
- Тетерин Г.Н. «Геометрическое» и «Геофизическое» в геодезии // Вестник СГГА. – 2011. – Вып. 1 (14). – С. 26-33.
- Тетерин Г.Н. Символ устаревшей идеологии // Вестник СГГА. – 2012. – Вып. 1 (17). – С. 47-52.
- Тетерин Г.Н. О координатизации – термине и понятии // Вестник СГГА. – 2012. – Вып. 4 (20). – С. 32-41.
- Тетерин Г.Н., Синянская М.Л. Биографический и хронологический справочник (Геодезия, картография – двадцатый век), Том II – 2012. – 592 с.
- Тетерин Г.Н. Четыре парадигмы и законы развития геодезии // Изв. вузов. «Геодезия и аэрофотосъемка». –2012 –№ 4. –С. 30–34.
- Тетерин Г.Н., Синянская М.Л. Геометрическая концепция и теория развития (предопределенности) геодезии // Новосибирск, СГГА. – 2014. – с 239.