УДК.528.001
Г.Н. Тетерин
СГГА, Новосибирск
КОНСТАНТЫ РАЗВИТИЯ И ТОЧКИ ПРОГНОЗИРОВАНИЯ
Любая система знаний, ее уровень развития характеризуется определенным набором констант. В их значениях заложены закономерности развития. Эти константы могут играть роль опорных точек прогноза. В статье приводятся константы и соответствующие прогнозы относительно общего развития знаний, различных информационных систем, темпов развития (например, по точности и эффективности – у = a × b-1). Приведены характеристики и сделаны некоторые прогнозы по координатизации пространства, по геодезическим информационным системам. Используя критерий идентификации, приведено три варианта констант и соответствующих алгоритмов прогноза.
точка прогнозирования, критерий идентификации, информация, условия координатизации, константы роста (развития), фундаментальные константы.
Любая система знаний характеризуется рядом числовых показателей, оценивающих достигнутый ею уровень развития. В исторически меняющихся показателях и их значениях заложены закономерности развития, при знании которых становится возможным прогнозирование. Эти константы являются своего рода опорными «точками прогноза». Эти же константы показывают глубину проникновения в те или иные явления природы, антропогенные или техногенные процессы. При этом для каждого этапа развития характерны свои числовые значения констант. Так для Древнего времени многие известные и использовавшиеся константы были характеристиками антропного происхождения, позднее — технологического и планетарного.
Для любой системы научных и профессиональных знаний, в том числе и для геодезии, можно подобрать совокупность таких показателей (по тому или иному признаку), которая остается сравнительно неизменной и вполне определяемой для какого-либо исторического периода развития. При сохранении неизменности своих значений не исключено, что эти параметры в целом на этапе исторического развития могут меняться (уточняться) в пределах какого-либо интервала – «коридора» значений (см. например, «коридор точности» [2]).
Чем выше уровень развития, чем разнообразнее сферы деятельности, тем разнообразнее параметры (константы), используемые и применяемые в этих сферах. В каждой области знаний есть специфические характеристики, используемые только в ней. В любой науке имеются свои наборы констант, соответствующие их объектам, предмету, методам, основным принципам и критериям.
Вместе с тем, используемый набор констант в каждой сфере деятельности может быть пополнен. Получение новых констант — это подчас результат исследовательской работы нескольких поколений ученых. Возрастание числа констант и их разнообразие — это рост эффективности науки, производства, это достижение новых рубежей в развитии и прогрессе, это новые возможности прогнозирования. Среди констант по их значимости выделяют фундаментальные, используемые, как правило, в нескольких науках. Для каждой эпохи они дают картину окружающего мира, слепок, модель этого мира, отвечающую духовным достижениям эпохи, глубине и широте проникновения человеческого разума в окружающий мир.
В конце XX в. получило распространение понятие фундаментальных геодезических постоянных (параметров Земли): геоцентрическая гравитационная постоянная fM (f — постоянная тяготения, М — масса), экваториальный радиус а, угловая скорость w и гармонический коэффициент второй степени и нулевого порядка j2.
Основы физических теорий составляют три фундаментальные постоянные: скорость света (3×1010 см/с), постоянная Планка (h = 10-27 гсм2 с-1) и ньютоновская постоянная (G = 7×10-8 г-1 см3 с-2) (Тетерин Г.Н. Памятные даты // Геодезия и картография. – 1995. – № 3. – С. 58). Из комбинации этих постоянных можно получить размерности длины, времени и массы.
Рассматриваемые ниже константы можно разделить на 2 группы (по отрезку времени): 1) на константы, характеризующие темпы изменений (в допустимом коридоре), прогресса между историческими эпохами (общевременные константы, константы изменений); 2) константы явлений, процессов, присущих данному историческому времени, эпохе, этапу, — константы данного этапа. Кроме того, константы можно подразделить также на моноконстанты и их производные.
Приведем примеры общевременных констант. Обратимся, например, к общеисторическим характеристикам. Пусть Тi — длительность развития между научными (техническими) революциями i-го периода, ti — длительность научной (научно-технической) революции.
Пусть T1 ≈ 8 000 лет — период развития общества от времени перехода человека к земледелию и скотоводству до начала греческой античной науки (VI в.
до н.э.); Т2 = 1 600 — 1 700 лет — период между концом греческой научной революции (II в. до н.э. включительно) и Великой научной революцией (XVI — XVII вв.); Т3 = 300 лет — период между научными революциями XVI — XVII вв. и XX в. (конец XIX в. — середина XX в.); t1 = 1 000 лет — техническая революция, обусловившая переход от кочевого образа жизни к оседлому; t2 = 400 лет — период греческой научной революции (VI-II вв. до н.э.); t3 = 150 — 200 лет — Великая научная революция (XVI-XVII вв.); t4 = 70 лет — научно-техническая революция (конец XIX — середина XX вв.).
С учетом приведенных значений получим
Уi = Ti / ti+1 = {20, 10, 4} (при i = 1, 2, 3);
ti / ti+1 ≈ 2,5 (при i = 1, 2, 3) и Ti / Ti+1 ≈ 5 / 6.
Следовательно, темпы сокращений в периодах T и t от эпохи к эпохе характеризуются значениями примерно в 6 и 2,5 раза, темпы сокращений их отношений Ti / ti+1 — в 20, 10, 4 раза.
Некоторые виды констант приведены в табл. 1.
В книге [2] для расчета уровня организации территории получен ряд формул, в том числе
Δу12 = 23n(2)-1 × a(2) × N3(2), (1)
Δу13 = 23n(3)+3n(2)-2 × a(2) × a(3) × N3(2) × N3(3), (2)
где Dу12, Dу13 — изменения уровня организации при переходе от первого этапа развития соответственно ко 2-му и 3-му; n(i) = {n(2), n(3)} — число удвоений функционального разнообразия на i-м этапе (i = 1, 2); a(i) = {a(2), a(3)} — функция, характеризующая число функциональных групп, на которые разбивается общее количество элементов N данной системы (или число групп).
Если положить:
a(1) = 10, a(2) = 102, a(3) = 104;
N(1) = 10, N(2) = 102, N(3) = 1010;
n(1) = 3, n(2) = 5, n(3) = 10,
тогда с учетом формул (1) и (2), получим
Δу12 » 2 × 1012; Δу13 = 1053.
Из табл. 1 можно получить параметры развития, константы, характеризующие темпы развития — Δуi j = уj /уi .
Результаты приведены в табл. 2.
Таблица 2 Константы развития (темпы роста)
| Параметры и характеристики |
Уij= Уj / Уi | |||
| ΔУ12 | ΔУ23 | ΔУ34 | ΔУ45 | |
Уровень потребленияУровень скорости Размер системыУровень организации Уровень сложности |
101-102
10 108 1010 1016 |
102-103
104 108-1010 1016-1017 1020 |
103
103 108-1010 1014 1016 |
104
104 1012 1016-1017 1018 |
Введем мультипликативные показатели (константы), отражающие разные факторы воздействия на процессы и оцениваемые системы. Например, воспользуемся оценкой типа
У = an bm. (3)
Пусть a — производительность труда в каких-либо условных единицах (или уровень экономической эффективности), b — точность измерений, n = 1, m = -1. Тогда
У = a b-1. (4)
Пусть У(i) — оценка i-го этапа развития. Тогда
ΔУ = У(i)/У(i+1) = (ai/ai+1) (bi+1/bi) = Δai/Δb, (5)
где Da — рост производительности труда (экономической эффективности) при переходе от i-го этапа развития к i + 1 (от одной эпохи к другой), Db — рост точности измерений при том же временном переходе. Из работ [1 — 5] известно, что при переходе от Древнего мира к Новому и от последнего к Новейшему точность выросла на 2 порядка (по некоторым переменным больше). В оценке Da для этих же интервалов многое зависит от единиц оценки. Но в общем случае порядок роста примерно такой же. И поэтому
ΔУ = Δa/Δb —>1. (6)
Используя ту же мультипликативную форму оценки, возьмем комбинацию констант и параметров (из области координатизации пространства — КП) вида
У = m×T / N, (7)
где m — число измеряемых величин (применительно к используемой системе координат) или размерность пространства (системы координат — СК), Т — уровень точности измерений (порядок точности, например 1 × 10-2 — Т = 2); N — число параметров, характеристик, необходимых при формировании и внедрении глобальной СК в заданном окружающем пространстве. Формула (7) характеризует условия координатизации пространства. В качестве пространства для расчетов по формуле (7) возьмем для Древнего времени ойкумену и ей соответствующую СК, определявшихся системой межевых линий (Древний Рим) или географической СК. Для Нового времени в качестве примера такой системы примем СК-42. Тогда для Древнего, Нового и Новейшегого периодов получим следующие значения m, T, N и У (табл. 3).
Таблица 3 Характеристики условий координатизации пространства
| Время | Компоненты формулы (7) | У | ΔУ = Уi / Уi+1 | ||
| m | T | N | |||
| Древнее
Новое Новейшее |
2
3 4 |
3
5 7 |
4
9* 18 |
1.5
1.6 1.6 |
1
1
|
Для Нового времени в m (m = 3) входят в качестве измеряемых величин расстояние, угол, атмосферное давление (или какая-либо другая величина, позволяющая определить высоту или превышение) или три размерности; N — число геодезических дат, T — порядок точности («коридор точности» этого времени: 10-4 — 10-6 [2]).
Для Новейшего времени (конец XX в.), исходя из m = 4, T = 7 и предполагаемого У = 1.6, получили значение N = 18. При этом значение У = 1.6 явилось опорной точкой прогноза.
Некоторые закономерности, выраженные в константах и характеристиках развития, при переходе от одного исторического этапа к другому автором были определены и опубликованы ранее. Так, известно, что ряд характеристик при историческом развитии по этапам меняется на единицу (размерность СК или пространства, порядок уравнения линии, поверхности — линии и поверхности первого порядка, затем второго); другие на 2 (порядок точности измерений [2], экономическая эффективность). Некоторые комплексные характеристики — типа (4) и (7) — можно принимать в качестве опорных точек прогноза, предполагая, что они сохраняют постоянство, как, например, значения У
и ΔУ в (4), (5) и в табл. 3.
Приведенные величины (У, ΔУ и др.), конечно, нельзя считать абсолютно точными. Как было сказано выше, они имеют какой-то свой «коридор» разброса.
По аналогии с выражением (7) (условие КП), можно ввести комплексную характеристику координатизированности пространства (уровень его структуризации), например, в виде
У = P × T × m × L,
где P — плотность КП, Т — точность, m — размерность СК, L — трудоемкость или эффективность КП.
Следует отметить одно интересное обстоятельство. Значение выражения равно единице. В нем Δa и Δb одинаковы по величине порядка и определяют рост эффективности и точности на 2 единице. Очевидно, эти 2 порядка разделяют эпохи — после количественного роста на 2 порядка наступают качественные преобразования. Возможно, именно это характеризует рубежи эпох, границы количественного накопления, после которого происходит качественное перерождение, своего рода «взрыв». Эти показатели являются константами перехода к новым эпохам.
В плане принципов координатизации и геометризации, в прикладной геодезии созданы системы приборов с соответствующими параметрами контроля и соблюдения таких геометрических свойств, как прямолинейность и плоскостность. Числовые значения этих характеристик составляют определенную группу констант.
Рассмотрим темпы изменений в росте объема информации на графических и машинных носителях. Сейчас количество информации в ГИС характеризуется числом тематических слоев. В цифровой карте масштаба 1 : 1 000 000 (США)
заложено 17 слоев. В электронных атласах сейчас насчитывается до 20 тематических слоев. Если число слоев обозначить буквой a, то ее значение в Древнее, Новое и Новейшее время будет соответственно a1 = 3, a2 = 7, a3 = 20… В каждом слое объем информации обозначим буквой ni (i = 1, 2, 3). При переходе от эпохи (i) к эпохе (i + 1) порядок n удваивается. Тогда общее количество информации Ni (полагая, что в доисторическое время оно было равным n0):
N1 = 3(n02); N2 = 7(3n02)2; N3 = 20(7234n08). (8)
Из (8) получим первые (Δi,i+1 = Ni+1/Ni) и вторые разности:
Δj(j+1) = Δj+1 / Δj,
где Δj = Δi,i+1.
При этом
Δ12 = 3n0i; Δ23 = 2 × 10n02; Δ34 = 2 × 103n04,
Δ34/Δ32 = Δ12‘ = 102n02; Δ34‘ = 104n4.
С учетом (8) и разностей Δi,i+1 и Δj,j+1‘ получим прогнозные значения
N4 = 4 × 103 × n016, отсюда следует число слоев a ≈ 4 × 103.
Если n0 = 10, то количество информации на графическом, машинном или каком-то другом носителе будет следующим:
N1 = 3 × 102; N2 = 6 × 105; N3 = 7 × 1012; N4 = 4 × 1019.
Рассмотрим характеристики уровня геометризации или геометрической идентификации различных явлений окружающего мира, т.е. их идентификацию геометрическими фигурами или моделями (графическими, цифровыми — каталогами, ЦМС и др.). Геометризация пространства (его структуризация) наиболее ярко выражается на графических моделях (картах) условными знаками.
В 1954 г. насчитывалось 460 условных знаков, а в 1977 г. их было 589.
В электронных моделях сейчас используется (по последним сообщениям (1998 г.)) до 256 оттенков. Если к условным знакам добавить принятые на картах сокращения, то уровень структурности, уровень геометризации характеризуется значением: на 1954 г. – 1 054, на 1977 – 1 390 (1 400). В среднем за 1/4 века произошло увеличение в 1,5 раза.
По координатной оценке уровня информативности, описанной в работах [3, 4], количество информации на листе карты масштаба 1 : 25 000 для равнинного малонаселенного района было получено равным Jр = 52 196, а для горного — Jг = 17 8851 ~ 180 000. При этих данных
Jр/M » 2.1; Jг/M » 7.1,
где M — знаменатель масштаба. Таким образом, в какой-то мере коридор значений (2.1 – 7.1) характеризует насыщенность информацией карт данного масштаба — 1 : 25 000.
Если число условных знаков a и число используемых сокращений b взять равным (на 1954 г.) 1 050, то для двух рассматриваемых районов получим:
Jг/(a + b) = 180 000/1 050 » 170,
Jр/(a + b) = 52 200/1 050 » 50. (9)
Таким образом, уровень выраженности условных знаков в единицах информации определяется для районов с различным рельефом диапазоном (50 — 170). Если увеличить полученные значения в 1,5 раза (для 1977 г.), получим диапазон (75 — 255).
Уровень отображения геометрической (и качественной) структуры пространства можно представить значением:
X = (a + b) × g, (10)
где g — число слоев (тематических).
За последние 30 лет уровень структурного отображения пространства возрос более, чем на порядок.
Одним из основных принципов формирования и развития геодезии является принцип геометризации знаний, объектов, местности, способов измерений [1]. Вообще можно полагать, что принцип возможности (или невозможности) выполнения геодезических измерений опирается на два условия: идентификацию и геометризацию. Под идентификацией понимается установление вообще наличия какого-либо явления и его пространственно-временное выделение, фиксация. Геометризация каких-либо объектов или явлений в общем случае означает их идентификацию какой-либо геометрической фигурой, моделью, пространственным отношением с той или иной степенью приближения (точностью). Точность моделей и измерений определяем теоретической и практической точностью геометризации.
В работе [2] приводится критерий идентификации
T(Δx) = [d(x2) — d(x1)] / Δp, (11)
где T(Δx) — критерий перехода в новую эпоху, признак необходимости формирования новых технологий, методов, принципов получения точной идентификации;
d(x) — фундаментальные постоянные, константы, параметры пространства, объекта; критические величины проявления объекта;
Δd = (d(х2) — d(x1)) — предельная или критическая величина изменений
в метрике объекта в интервале [x1, х2], характеризующая порог доступности для исследований или определяющая качественный, возможно катастрофический, переход в новое состояние объекта;
Δp — критический интервал изменений в метрике, доступный для геодезических измерений (точность измерений).
Согласно (11), объект, явление идентифицируется с момента, когда T(Δx) > 1. Для этого критерия возможны три группы значений:
> 1 — явление идентифицируется,
Т(Δх) < 1 — явление не идентифицируется, (12)
= 1 — явление идентифицируется сомнительно
(граница идентификации).
С учетом обозначений
Т(x) = Δd(x) / Δp(x). (13)
Рассмотрим три варианта использования (13):
- Δd и Δp — переменные, являющиеся функциями соответственно f1(x) и f2(x);
- Δd = f1(x), Δp = const;
- Δd = const, Δp = f2(x).
- В первом варианте примем [2]:
df1(x) / dx = a и df2(x) / dx = bx.
Тогда
f1(x) = a(x2 — x1); f2 = b(x22 — x12) / 2.
Отсюда
Т(Δx) = c / (x2 + x1) ³ 1, (14)
где с = 2а / b.
При x2 = lx получим
[c / x(1 + λ] ³ 1 или [x / (1 + λ)] ≤ c.
Следовательно,
λ ≤ (c / x) — 1, λ ≤ (c — x) / x (15)
или x ≤ c / (1 + λ)
При этом величины x или λ есть критические точки или константы идентификации. Соответствующие примеры приведены в [2].
- Примем Δp = const, Δd = f1(x).
В соответствии с (12) и (13), явление идентификации при Т(Δx) < 1
Δp ≤ d(x2) — d(x1).
В качестве примера этого варианта приведем историческое событие — французские градусные измерения двух поколений Кассини, не подтвердившие полярное сжатие Земли, вытекавшее из теории Ньютона. Причины этой ошибки рассмотрены Ф.Н. Красовским.
Д. и Ж. Кассини, Маральди и Лаир выполнили измерение двух дуг меридиана, из сравнения которых собирались сделать вывод о сжатии Земли. Закончив градусные измерения в 1701 г. и обработав их, они получили ошибочный результат — Земля сжата по экватору. Ф.Н. Красовский показал (Руководство по высшей геодезии. — М., 1942, — ч. II, 560 с.), что разность длин дуг (северной и южной) составляла 40 тоазов. В то же время, ошибка в определении широт была равна 4″(32 тоаза). Если учесть все другие источники ошибок,
в том числе уклонения отвесных линий, то получим Δp > Δd, т.е.
Т = Δλ / Δp < 1.
Таким образом, сжатие не могло быть идентифицировано. Отсюда ошибка Кассини, приведшая к длительным спорам, закончившимся почти через 50 лет.
В то же время, если взять две дуги меридиана на широтах 00 и 880 (широты Перуанской и Лапландской экспедиций, то разность длин дуг меридианов будет 600 тоазов (1 120 м), и тогда условие выполняется, т.е. Δp < Δd, и поэтому
T(Δx) > 1.
III. Примем Δd (x) = const, Δp = f2 (x). Примем изменение f2 (x) обратно пропорциональным времени.
Пусть
df2(x) / dx = a / x. (16)
Тогда
f2(x) = aln(x2 / x1) = aln(λ), (17)
где λ = x2 / x1.
С учетом (12) и (13), а также обратно пропорциональной зависимости изменения времени и точности, критерий идентификации получит вид
T(Δx) = Δd / Δp = Δd / alnl ³ λ.
Таким образом,
λ ≤ e d/a . (18)
Пусть x1 и xe есть время, т.е. соответственно t1, t2, Dt = t2 — t1 — промежуток времени идентификации. Исходя из условия варианта, имеем Δd = const. Требуется дать прогноз, когда данное явление будет идентифицировано? Имея в виду, что l = t2 / t1, получим
t2 ≤ t1 ebDd , (19)
где b = 1/a, t2 = t1 + Δt, Δt — период прогнозирования.
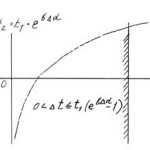
На рисунке показана область идентификации Δp ≤ Δd (или область прогнозирования Δt)
0 < Δt ≤ t1(eb Dd — 1). (20)
Таким образом, начиная с момента t2 = t1 + Δt, явление может быть идентифицировано, при этом Δt — это прогнозируемый промежуток времени.
Решающая роль геометризации в развитии геодезии предполагает наличие возможности установления оценки этого процесса. Оценка уровня геометризации, характерная для данного исторического этапа геодезических измерений, может стать формой и содержанием оценки развития геодезии. Числовые значения такой оценки могут играть роль параметров, констант развития или параметров обновления.
Достигнутая точность в какой-то мере характеризует одновременно и геометризацию, и идентификацию объектов измерений и самих измерений и является своего рода фундаментальной характеристикой, параметром развития геодезии данного периода.
Уровень развития геодезии в какой-то мере соотносится с масштабом обживаемого пространства или его качественной стороной [2] (естественная среда обитания, техносфера, ближний космос). В каждом из трех пространств на данном этапе освоения существуют свои условия измерений, их пределы, ограничения и, следовательно, свои константы. Показательна в этом отношении таблица констант, приведенная в работе [5].
СПИСОК ЛИТЕРАТУРЫ
- Тетерин Г.Н. История геодезии. — Новосибирск: НИИГАиК, 1990, ч. I, 67 c.
- Тетерин Г.Н. История развития геодезии. — Новосибирск: СГГА, 1999. — 276 с.
- Тетерин Г.Н. Информационная структура некоторых видов карт //Геодезия и картография. — 1982. — № 9. — C. 43 — 45.
- Тетерин Г.Н. Информационные характеристики карт // Изв. вузов. Геодезия и аэрофотосъемка. — 1986. — № 3. — С. 89 — 94.
- Тетерин Г.Н. О точности геодезических измерений (исторический аспект, тенденции развития) // Геодезия и картография. — 1997. — № 8. — С. 49 — 53.