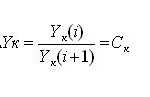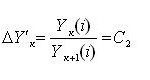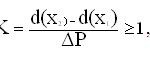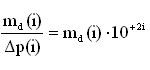Г.Н. Тетерин
УДК 528 (091), 528 (092).
Четыре парадигмы и законы развития геодезии.
Понимание настоящего приходит через прошлое, через историю. В свою очередь виртуальное, интеллектуальное проникновение в будущее становится возможным только на основе изучения истории развития, установления законов развития, заложенных в окружающий мир и общество. Для понимания процесса развития науки необходимо построить некую историческую последовательность и установить для нее соответствующую закономерность в рамках допустимой точности.
Система геодезических знаний является исторически не только самой древней, но и одной из самых востребованных. По существу, истоки геодезических знаний были заложены (с точки зрения их предметной сущности) еще с доисторических времен. Доказательство этого заключено в «принципах влияния» (ПВГ и П4Н) [1], которые существенным образом определяли жизнь человека и общество.
Законы развития диктовались пространством и временем, в рамках которых существовал человек. Поскольку предметом геодезии является геометрия окружающего физического пространства, отсюда следует значимость науки и сферы профессиональных геодезических знаний.
Законы развития геодезии формировались как на основе упомянутых двух «принципов влияния», так и на основе принципов геометризации и координатизации, а также в рамках социально-экономического развития общества. Технологические и теоретические закономерности развития геодезии на протяжении всей истории подробно описаны в работах [1, 3, 4], в частности, эти закономерности ярко представлены и выражены в таблице 1.
Развитие науки, системы знаний характеризуются такими законами как неравномерность, цикличность и революциями (обновление знаний). В геодезии это наглядно характеризуется ступенчатообразной кривой (Рис.1). Эти три закона развития хорошо укладываются в понятие парадигмы, которая ярко характеризует каждый исторический этап развития. Как известно, парадигма – это понятийно-терминологическая основа (базис) системы знаний. Переход одной парадигмы в другую проходит на основе кардинальных революционных преобразований в теории и практике, в целом всей системы знаний.
Таблица 1. Характеристики исторических этапов развития геодезии
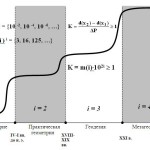 Рис. 1. Закон логистического развития геодезии
Рис. 1. Закон логистического развития геодезии
Система геодезических знаний в своем историческом развитии имеет в прошлом три этапа (исторические эпохи, циклы), в каждой из которых сформировалась своя парадигма (таблица 2). Переход от одной парадигмы к другой совершается путем революционного обновления всей системы теоретических и практических знаний. Сейчас реализуется новая, четвертая парадигма [1], характеризуемая новыми теоретическими и методологическими основами [1, 5].
Обновление терминологии связано с появлением новых методов, систем измерений и моделирования. Обновление системы знаний и формирование парадигмы происходит за счет усиления абстрактности, строгости и обоснованности в теории, за счет увеличения влияния упомянутых выше четырех системных принципов. К факторам, оказывающим влияние на обновление, относится расширение используемого физического пространства за счет принципиально новых методов: геоинформационных, дистанционных и т.д. Новый, более строгий предметный подход к теории геодезии, позволяет ввести новый системный уровень в систему совокупности геодезических методов и подходов до уровня трех основных задач геодезии: определение (измерение), моделирование и контроль геодезической метрики объектов и явлений окружающего пространства [1, 5].
В основе последнего направления геоинформационного обновления геодезии (конкретность, системность, строгость) лежит введение понятий структурных элементов и пяти групп постулатов [1, 5].
В рамках этих постулатов, понятий структурных элементов, естественно, формируется понимание и определение геодезии [1, 4], не вступающее в противоречие с прошлым геодезии, ее историей. В последнем случае возникает явное (диалектическое) противоречие между классическим пониманием и объяснением геодезии и новым подходом, использованием концепции, получившей название геометрической.
Автором разработана аналитическая модель прогноза по историческим эпохам, парадигмы которых приведены в таблице 2 и на Рис. 1.
На основе накопленных исторических данных по результатам прошедших трех исторических эпох и их численных показателей автором разработаны эмпирические аналитические формулы, отражающие существующие закономерности и законы развития. Одной из важнейших закономерностей такого рода развития служит функциональная зависимость
Y = f(i) (1),
где Y – эффективность, характеристики, параметры исторической эпохи (например, точность метрических геодезических измерений);
i – номер исторической эпохи: i=1 – землемерная, i=2 – геометрическая (римско-эллинистическая), i=3 – топографо-геодезическая, i=4 – новейшая эпоха, геоинформационная, глобальная.
Для зависимости (1) автором ранее были получены следующие формулы:
Обозначим Y1 – точность измерений,
Y2‘- размерность системы координат,
Y2»- число начальных дат,
Y3 – число используемых CК.
Для введенных обозначений получим:
Y1=10-2i, (2)
Y2‘=i, Y2»=i2, (3)
Y3 = (2 + i)i (4)
Применительно к точности измерений с учетом (2) для каждой исторической эпохи получаем используемый коридор точности измерений.
ΔY1(i) = {10-2(i-1) – 10-2i} (5)
Применительно к каждой исторической эпохе этот коридор точности имеет вид:
до 10-2 при i = 1
от 10-2 до 10-4 при i = 2
ΔY1(i) = от 10-4 до 10-6 при i = 3 (6)
от 10-6 до 10-8 при i = 4
В работе [6] даны коридоры точности для разных эпох, систем измерений и технологий.
Аналогичные «коридоры» используются в каждой исторической эпохе по другим параметрам.
Переход от одной ступени развития к другой (своего рода «скачек» развития) характеризуется отношением:
где к = 1, 2, 3.
Применительно к точности измерений и формуле (7) «скачек» в точности измерений при переходе от эпохи к эпохе будет иметь вид:
ΔY1(i)= 10-2i/10-2(i+1) = 102 (9)
Таким образом, переход от эпохи к эпохе сопровождается повышением точности на два порядка. В случае Y3 количество используемых СК возрастает примерно на один порядок. Если требуется определить в какой эпохе возможно реализовать заданную точность измерений применительно к какому-либо объекту измерений, то можно применить критерий идентификации [2]:
где К – критерий идентификации;
d(x) – константы, параметры, характеристики, фундаментальные постоянные пространства или его отдельных объектов;
x1, x2 – моменты времени, или какие-либо другие метрические аргументы, параметры;
d(x2) – d(x1) – предельная или критическая величина в интервале x2 — x1, определяющая качественный переход или изменение в состоянии объекта (явления);
ΔP – критический интервал в метрике того же объекта за период Δx = x2 — x1, доступный для геодезических измерений.
В работе автора [2] приведены примеры различного использования этого критерия.
Если в формуле (10) числитель обозначить как d(x2) – d(x1) = Δd и выразить в относительной мере , а в знаменатель Δр = Δр( i ) = 10-2 i, то получим
где i – эпоха, этап развития (i = 1, 2, 3, 4, 5).
Примем в качестве примера использования критерия идентификации применительно к точности определения размера Земли (ее радиуса или полуосей). Соотнесем эту точность с исторической эпохой, временем. Если точность определения радиуса Земли = 0.1 км, то mi=1,5·10-5.
Тогда при i = 3 (Новое время) K>=1, а при i = 2 (древнее время) K<1, т. е. точность не реализуется.
Таким образом, заданная точность в древнее время была нереальна. Для Нового времени критерий (10) выполняется как для 0.1 км, так и для 0.01 км (десятки метров). Эти результаты подтверждаются градусными измерениями этих эпох.
Для нашего времени (i = 4) критерий реализуется уже для субметровой точности. Действительно, к этой точности мы подошли в конце XX в.
Итак, точность определения размеров Земли в диапазоне метров – дециметров относится к времени, начало которого приходится на 90-е годы XX в. или на начало XXI в. Следующий интервал точности идентификации Земли приходится уже на следующую историческую эпоху, так как > 1 (при i = 5)
Несомненно, представляет определенный интерес, в плане прогноза, временные рамки каждой исторической эпохи. Конечно, границы этих эпох «размыты» и даже, более того, условны. Тем не менее, они служат каким-то ориентиром в прогнозах как параметров этих эпох, так и временем перехода.
Обозначим продолжительность i-й исторической эпохи как ΔТi, а продолжительность революционной части данной эпохи как Δti. Тогда для введенных выше эпох I = 1, 2, 3 получим два следующих временных ряда [2]:
ΔТi = {8000,1600-1700, 300} (12)
Δti = {1000, 400, 150-160, 50} (13)
Приведенные значения очень приближенны. Темп смены эпох можно охарактеризовать коэффициентами:
λ = ΔТi / ΔТi+1 = {5,…,6} (14)
β = Δti / Δti+1 = 2,5 (15)
Имея (14) и (15) нетрудно определить границы эпох, их временные рамки [3, 4]
Тi+1 = Тi + ΔТi / λ (16)
Δti+1 = Δti / b (17),
где Тi — конец эпохи i.
Примем Т3 = 1990 (конец 3-ей эпохи).
Тогда Т4 = Т3 + ΔТ3 /5 ≈ 2050г.
При λ = 6 имеем 2040г.
Конечно, полученные цифры ориентировочны. Вместе с тем, приведенные расчеты служат неким показателем развития системы знаний, общим показателем и характеристикой развития. Интересно сопоставить продолжительность исторической эпохи с числом поколений ni, тогда в 4-ой эпохе, в которую мы вступили, укладывается приблизительно n4 ≈3; имея в виду, что l ≈5, получим:
n3=15; n2 ≈ 75-80; n1 ≈ 400.
В четвертой эпохе переход к 5-ой эпохе начнется с революционных изменений, которая наступит примерно к середине тридцатых годов 21-го столетия.
В рамках рассмотренных выше закономерностей формируются параметры, характеристики последующих исторических эпох. Вместе с тем все отмеченное правомерно и справедливо, если развитие геодезии и общечеловеческой системы знаний будет проходить по тем же «правилам», что и в прошлом при формировании предыдущих трех эпох развития.
Литература
- Тетерин Г.Н. Феномен и проблемы геодезии. /Новосибирск: СГГА, 2009.-95с.
- Тетерин Г.Н. Принципы, критерии, законы развития геодезии. Новосибирск: Сибпринт, 2002. – 104 с.
- Тетерин Г.Н. История геодезии (до XX в.). Новосибирск: СГГА, 2008. – 300с.
- Тетерин Г.Н. Теория развития и метасистемное понимание геодезии. Новосибирск: СГГА, 2006. – 162 с.
- Тетерин Г.Н. Геодезия — это метод, или «наука о фигуре Земли», или нечто большее?. //Изыскательский вестник, 2009, №2, с. 5-11.
- Тетерин Г.Н. Принцип Первопроходца, параметры развития.// Изв. вузов. Геодезия и аэрофотосъемка, 2004, №3. С. 48-57.